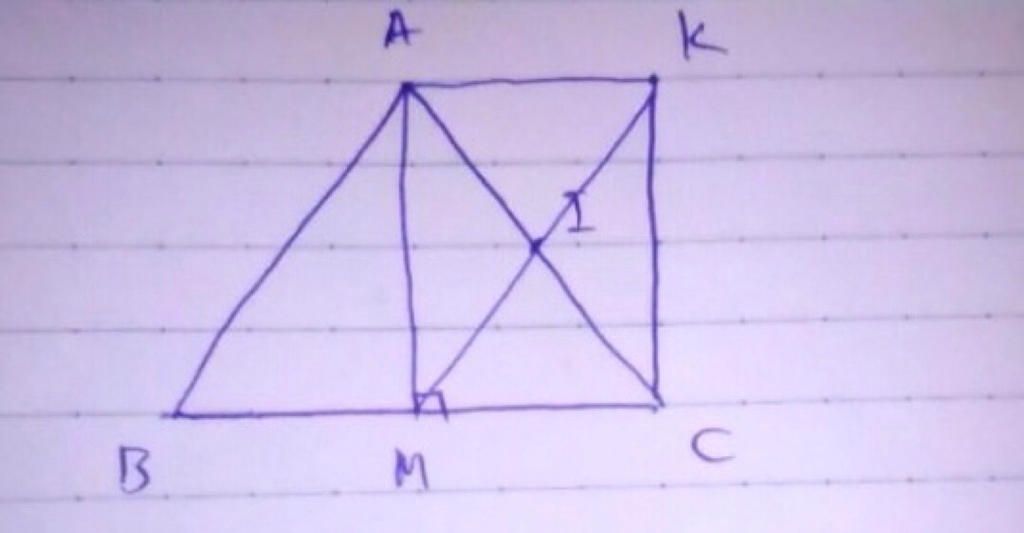
Toán Lớp 8: cho tam giác ABC cân tại A, đg trung tuyến AM. Gọi I là trung điểm AC, K là điểm đối xứng qua I
a) Tứ giác AMCK là hình gì?
b) Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông
Leave a reply
Register Now
Login
Lost Password
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Toán Lớp 8: cho tam giác ABC cân tại A, đg trung tuyến AM. Gọi I là trung điểm AC, K là điểm đối xứng qua I
a) Tứ giác AMCK là hình gì?
b) Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông
Comments ( 2 )
a,Xét tứ giác AKCM có:
MI=MK(K là điểm đói xứng với M qua I(gt))
IA=IC(I là trung điểm AC(gt))
AC giao MK tại I
=>AMCK là hình bình hành (1)
Vì tam giác ABC cân tại A (gt)
AM là đường trung tuyến (gt)
=>AM cũng là là đường cao (t/c)
=> Góc AMK=90 độ (2)
Từ (1)(2)=>AKCM là hình chữ nhật
b, Để AMCK là hình vuông
AMCK vừa là hình chữ nhật vừa là hình thoi
Mà AMCK là hình chữ nhật
Vậy ta cần tìm điều kiện để AMCK là hình thoi
Để AMCK là hình thoi
AM=MC
Mà MC=1/2BC(AM là đường trung tuyến của tam giác ABC(gt))
AM=1/2BC
tam giác ABC vuông tại A (tính chất về đường trung tuyến ứng với cạnh huyền)
tam giác ABC vuông cân tai A
Vậy muốn tứ giác AMCK là hình vuông thì tam giác ABC phải vuông cân tại A