Toán Lớp 8: Chứng minh hình bình hành có hai đường chéo bằng nhau là hình chữ nhật

Question

Toán Lớp 8:  Chứng minh hình bình hành có hai đường chéo bằng nhau là hình chữ nhật

ngoclanhoa · Answer

Hình bình hành có hai đường chéo bằng nhau
Ví dụ:
Cách 1:
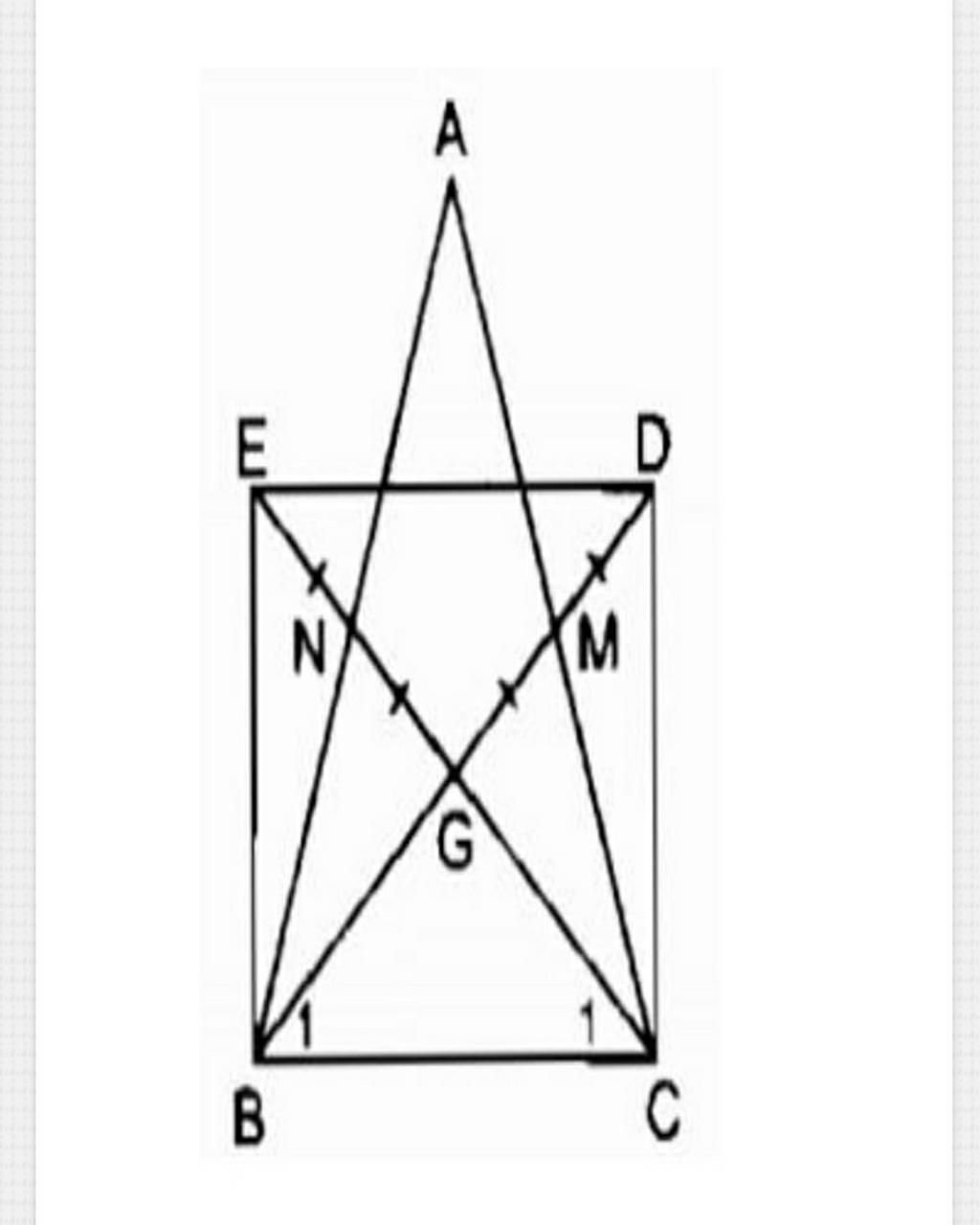
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?
Theo bài ra, ta có: G là trọng tâm của ΔABC.
⇒ GB = 2GM và GC = 2GN
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (3)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (4)
Từ (3) và (4) ⇒ Tứ giác BCDE là Hình bình hành do hai đường chéo cắt nhau tại trung điểm mỗi đường. (5)
Cách 2:
Xét ΔBCM và ΔCNB, có:
BC cạnh chung
Góc BCM = CBN (tính chất tam giác cân)
CM = BN (vì AB = AC)
Suy ra: ΔBCM = ΔCBN (c.g.c)
⇒ Góc B1 = C1 ⇒ ΔGBC cân tại G ⇒ GB = GC ⇒ BD = CE (6)
Từ (5) và (6), suy ra: BCDE là hình chữ nhật do là hình bình hành có hai đường chéo bằng nhau. ( đ.p.c.m )

Xin CTLHN ạ
toan-lop-8-chung-minh-hinh-binh-hanh-co-hai-duong-cheo-bang-nhau-la-hinh-chu-nhat