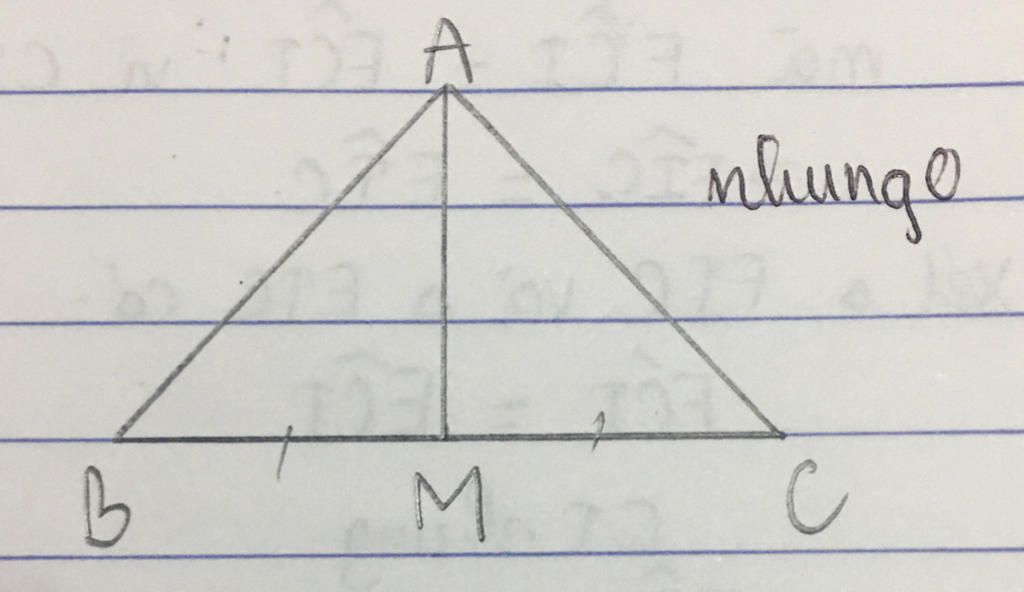Toán Lớp 7: Cho tam giác ABC cân tại A có cạnh AB =10cm và BC =12cm .Lấy M là trung điểm của BC
a) Chứng minh góc AMB =90 độ
b ) Tính AM
Leave a reply
Register Now
Login
Lost Password
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Toán Lớp 7: Cho tam giác ABC cân tại A có cạnh AB =10cm và BC =12cm .Lấy M là trung điểm của BC
a) Chứng minh góc AMB =90 độ
b ) Tính AM
Comments ( 2 )
$#QLinkVN$
a) Nối AM lại.
Xét \DeltaAMB và \DeltaAMC có:
AB=AC (\DeltaABC cân tại A)
MB=MC (M là trung điểm của BC)
AM: chung
=>\DeltaAMB=\DeltaAMC (c.c.c)
=>\hat{AMB}=\hat{AMC} (hai góc tương ứng)
Ta có:
\hat{AMB}+\hat{AMC}=180^{o} (hai góc kề bù)
Lại có: \hat{AMB}=\hat{AMC}
=>\hat{AMB}+\hat{AMB}=180^{o}
<=>2.\hat{AMB}=180^{o}
<=>\hat{AMB}=180^{o}:2
=>\hat{AMB}=90^{o} (đpcm)
b) Có BC=12cm và M là trung điểm của BC
=>MB=MC=(BC)/2=(12)/2=6 cm
Xét \DeltaAMB có: \hat{AMB}=90^{o}
=>\DeltaAMB vuông tại M
Xét \DeltaAMB vuông tại M
Áp dụng định lý Pytago vào \DeltaAMB, ta có:
AM^{2}+MB^{2}=AB^{2}
Thay MB=6cm và AB=10cm vào vế trên, ta có:
AM^{2}+6^{2}=10^{2}
<=>AM^{2}+36=100
<=>AM^{2}=100-36
<=>AM^{2}=64
=>AM=\sqrt{64}=8
Vậy AM=8cm
Đáp án
