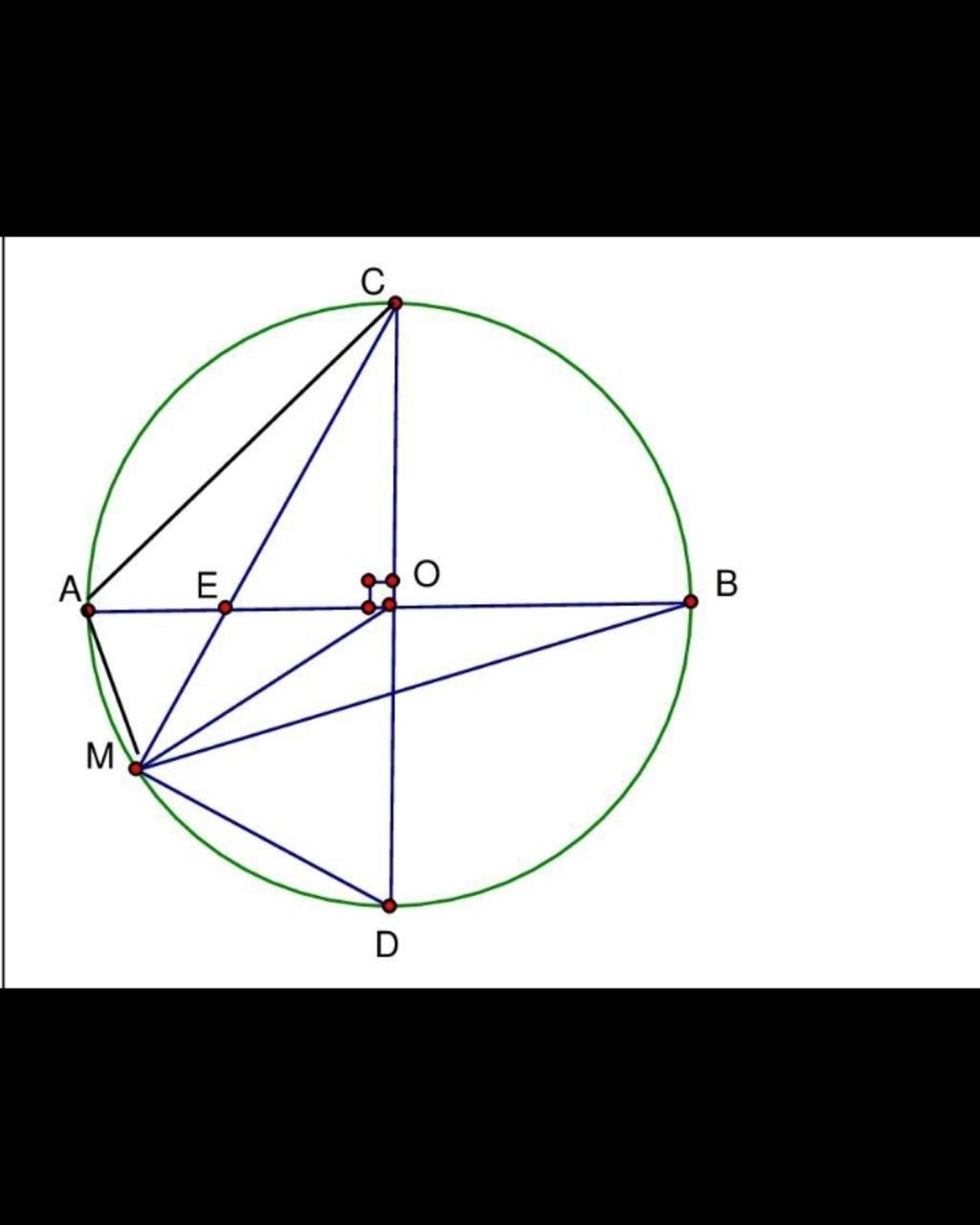
Toán Lớp 9: Cho đường tròn (O,R). Gọi AB và CD là hai đường kính vuông góc với nhau. Lấy M tùy ý thuộc cung nhỏ AD, vẽ CM cắt AB tại E.
A) Chứng minh: CE. CM =CO. CD
B) Hạ MQ vuông góc với CD tại Q, cắt đường tròn (O) tại điểm thứ hai N. Chứng minh: MN^2 =4 CQ. DQ
C) Điểm M nằm ở vị trí nào trên cung nhỏ AD để diện tích tứ giác MACB bằng diện tích tứ giác MCBD?
D) (Chỉ cần ghi sơ đồ chứng minh)
Tính số đo góc CMB.
Leave a reply
Comments ( 2 )
Đáp án
$\Delta CEO\backsim\Delta CDM\left( g.g \right)\Rightarrow CE.CM=CO.CD$
b)
$MN^2=4MQ^2=4CQ.DQ$
c)
Hạ $MF\bot AB$
${{S}_{MACB}}={{S}_{\Delta MAB}}+{{S}_{\Delta CAB}}$
${{S}_{MACB}}=\dfrac{1}{2}MF.AB+\dfrac{1}{2}CO.AB$
${{S}_{MACB}}=\dfrac{1}{2}AB\left( MF+CO \right)$
${{S}_{MACB}}=R\left( MF+R \right)$
Tương tự: ${{S}_{MCBD}}=R\left( MQ+R \right)$
Để ${{S}_{MACB}}={{S}_{MCBD}}$
Thì $MF=MQ$
$\Rightarrow OFMQ$ là hình vuông
$\Rightarrow OM$ là tia phân giác $\widehat{AOD}$
$\Rightarrow M$ là điểm chính giữa $\overset\frown{AD}$
d)
$\widehat{CMB}=\dfrac{1}{2}\text{sđ}\overset\frown{BC}=45{}^\circ $