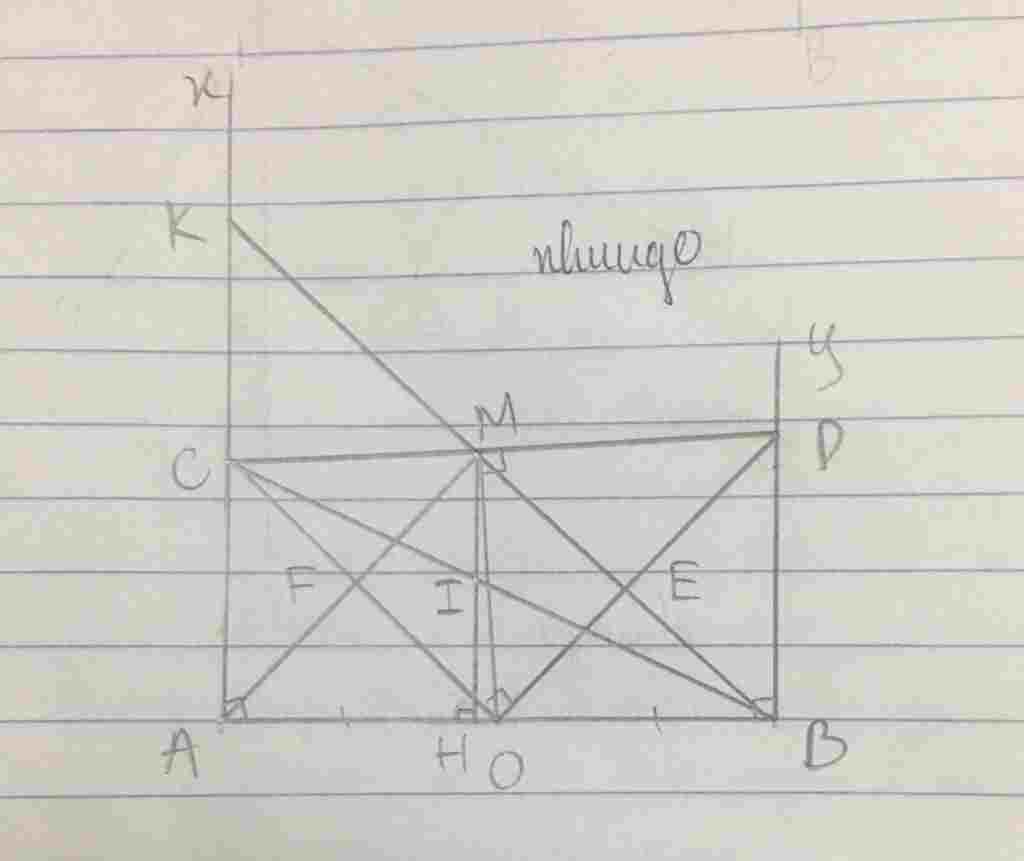
Toán Lớp 8: Cho O là trung điểm của đoạn AB . Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ tia Ax , By cùng vuông góc với AB . Trên tia Ax lấy điểm C (khác A) . qua O kẻ đường thẳng vuông góc với OC cắt tia By tại D
a, CM : AB^2 = 4 . AC . BD
b, Kẻ OM ⊥ CD tại M . CM : AC = CM
c, Từ M kẻ MH ⊥AB tại I . CM BC đi qua trung điểm MH
Leave a reply
Comments ( 2 )
$a,$ Xét $ΔAOC$ và $ΔBDO$ có:
$\widehat{CAO}=\widehat{DBO}$
$\widehat{AOC}=\widehat{BDO}(+\widehat{BOD}=90^o)$
$⇒$ $ΔAOC~ΔBDO(g-g)$
$⇒$ $\dfrac{OA}{BD}=\widehat{AC}{OB}$
$⇒$ $OA.OB=AC.BD$
$⇒$ $\dfrac{1}{2}.AB.\dfrac{1}{2}.AB=AC.BD$
$⇒$ $\dfrac{1}{4}.AB^2=AC.BD$
$⇒$ $AB^2=4.AC.BD$
$b,$ V $ΔAOC~ΔBDO(g-g)$
$⇒$ $\dfrac{AC}{OB}=\dfrac{OC}{DO}$
$⇒$ $\dfrac{AC}{AO}=\dfrac{OC}{DO}$
$⇒$ $ΔAOC~ΔDOC(c-g-c)$
$⇒$ $\widehat{OCA}=\widehat{DCO}$
$⇒$ $OC$ là đường phân giác $\widehat{DCA}$
Mà: $OM⊥CD,OA⊥CA$
$⇒$ $OM=OA$
$⇒$ $AC=CM$
$c,$ $CMTT:MD=BD$
Gọi giao của $BC$ và $AD$ là: $G$
$⇒$ $\dfrac{AC}{BD}=\dfrac{CG}{GB}=\dfrac{AG}{GD}=\dfrac{CM}{DM}$
$⇒$ $MG//AC$
$⇒$ $MG⊥AB$ tại $H$
Mà ta có:
$\dfrac{MG}{BD}=\dfrac{CG}{CB}=\dfrac{AG}{AD}=\dfrac{GH}{BD}$
$⇒$ $GM=GH$
$⇒$ $G$ là trung điểm của $MH$
Lại có: $AD∩BC=G$
$⇒$ $BC$ đi qua $G$ là trung điểm của $MH$
$⇒$ $ĐPCM$.
Đáp án
