Toán Lớp 8: 1) Cho biểu thức: A = (2x – 3)2 – (x + 1)(x + 5) + 2
Rút gọn và tìm giá trị nhỏ nhất của A.
2) Cho B = n2 – 27n2 + 121. Tìm số tự nhiên n để B là số nguyên.
Leave a reply
Register Now
Login
Lost Password
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Toán Lớp 8: 1) Cho biểu thức: A = (2x – 3)2 – (x + 1)(x + 5) + 2
Rút gọn và tìm giá trị nhỏ nhất của A.
2) Cho B = n2 – 27n2 + 121. Tìm số tự nhiên n để B là số nguyên.
Comments ( 2 )
1 nhé
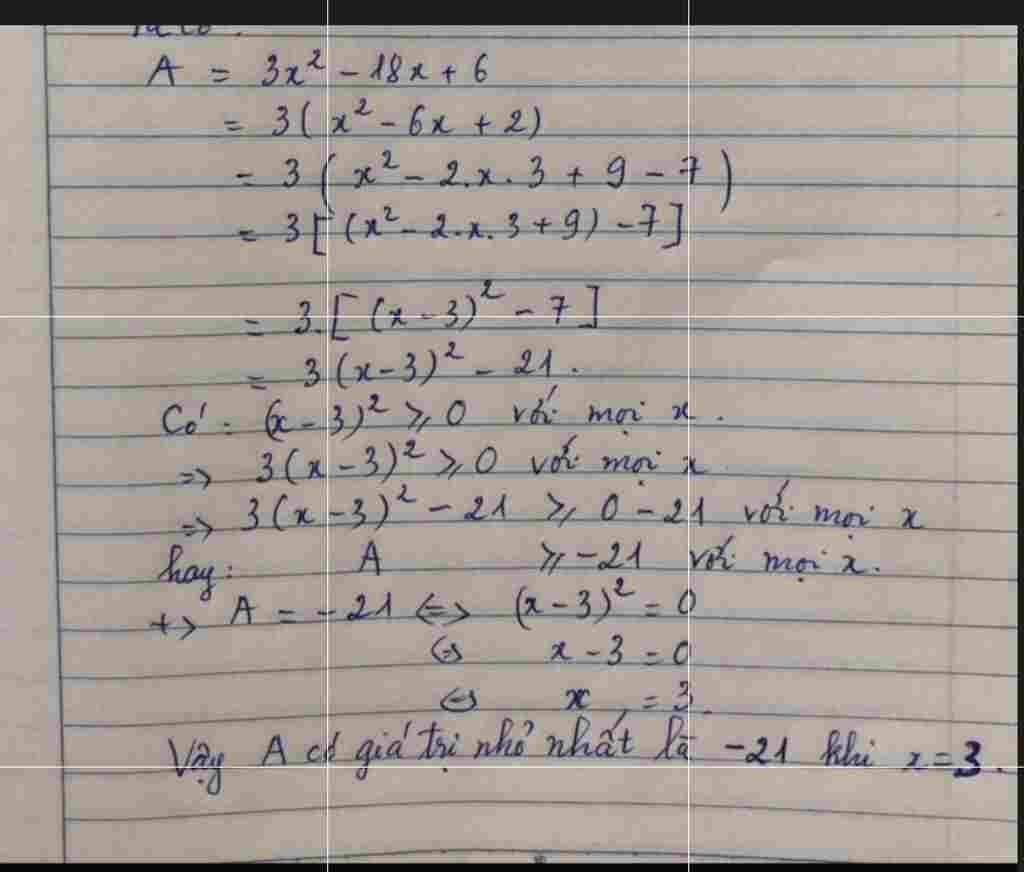
Giải đáp + Lời giải và giải thích chi tiết:
1)
A =$(2x – 3)^2$ – (x + 1)(x + 5) + 2
A = 4$x^2$ – 12x + 9 – $x^2$ – 6x – 5 + 2
A = 3$x^2$ – 18x + 6 = 3($x^2$ – 6x + 2)
A = 3$x – 3^2$ – 7 $\ge$ 3 . (-7) = -21
$\Rightarrow$ Dấu ” = ” xảy ra khi x – 3 = 0 $\Leftrightarrow$ x = 3.
$\Rightarrow$ A = -21 $\Leftrightarrow$ x = 3
2)
B = $n^4$ – 27$n^2$ + 121
B = $n^4$ + 22$n^2$ + 121 – 49$n^2$
B = $(n^2 + 11)^2$ – $(7n)^2$
B = ($n^2$ + 7n + 11)($n^2$ – 7n + 11)
Vì n ∈ N
$\Rightarrow$ $n^2$ – 7n + 11 > 1
Điều kiện B là số nguyên tố:
$n^2$ – 7n + 11 = 1
$\Leftrightarrow$ $n^2$ – 7n + 10 = 0
$\Leftrightarrow$ (n – 2)(n -5) = 0
$\Leftrightarrow$ $\left[\begin{matrix} n = 1\\ n = 5\end{matrix}\right.$
Nếu n = 2
$\Rightarrow$ B = 29 (số nguyên tố)
Nếu n = 5
$\Rightarrow$ B = 71 (số nguyên tố)
$\Rightarrow$ n ∈ { 2, 5 } $\Rightarrow$ giá trị cần tìm
۶ƙ¡ทջℳα₷Շℯℛ๖ۣۜ