Toán Lớp 7: Chờ tam giác ABC nhọn , gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=AM
a, Chứng minh ∆ AMB=∆DMC
b, Kẻ MH vuông góc với AB .Chứng minh : MH vuông góc CD
c, Gọi I là trung điểm của AB, P là trung điểm của CD . Chứng minh 3 điểm I; P;M thẳng hàng
Mọi người giúp mik vs , mik đang cần gấp????????????
Leave a reply
Comments ( 2 )
Bài đây em nhé
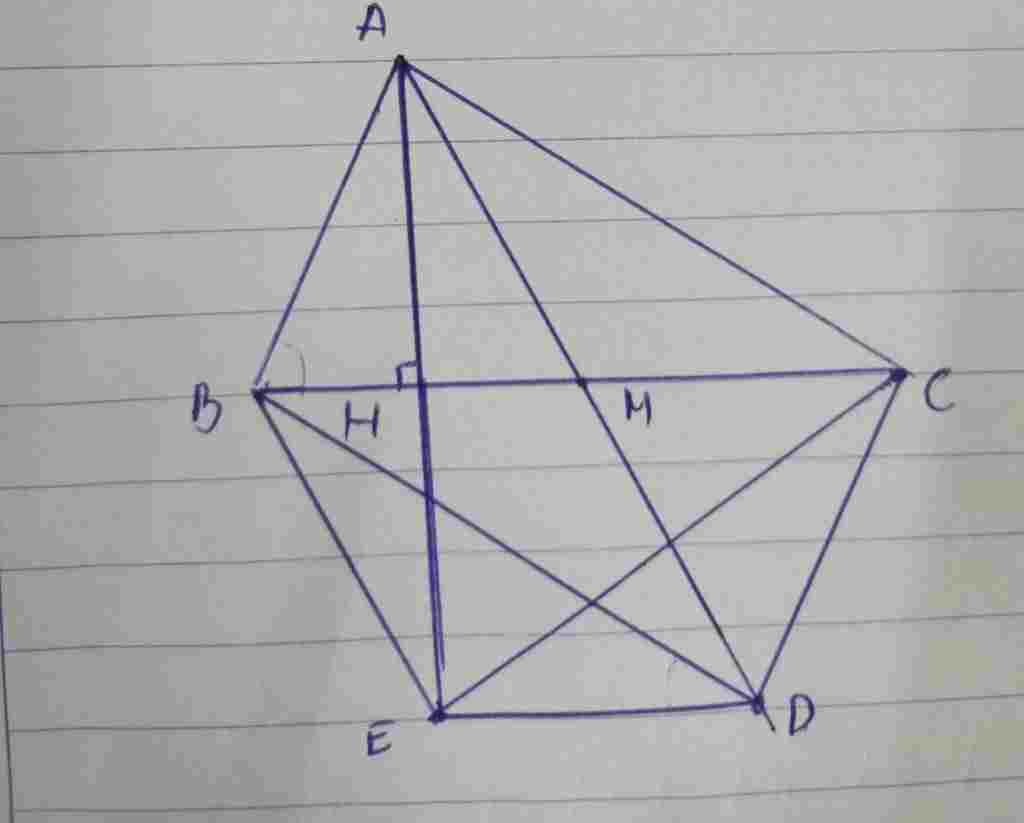
Giải đáp:
a) $\triangle AMB=\triangle DMC$
b) $MH\bot CD$
c) I, M, P thẳng hàng
Lời giải và giải thích chi tiết:
a)
Xét $\triangle AMB$ và $\triangle DMC$:
$AM=DM$ (gt)
$\widehat{AMB}=\widehat{DMC}$ (đối đỉnh)
$MB=MC$ (gt)
$\to\triangle AMB=\triangle DMC$ (c.g.c)
$\to AB=DC$ (2 cạnh tương ứng)
$\to\widehat{MAB}=\widehat{MDC}$ (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
$\to AB//CD$
b)
Ta có: $MH\bot AB$ (gt)
Mà $AB//CD$ (cmt)
$\to MD\bot CD$
c)
Ta có: I là trung điểm của AB, P là trung điểm của CD (gt)
Mà $AB=CD$ (cmt)
$\to AI=IB=CP=PD$
Xét $\triangle AMI$ và $\triangle DMP$:
$AM=DM$ (gt)
$\widehat{MAI}=\widehat{MDP}\,\,\,(\widehat{MAB}=\widehat{MDC})$
$AI=DP$ (cmt)
$\to\triangle AMI=\triangle DMP$ (c.g.c)
$\to\widehat{AMI}=\widehat{DMP}$ (2 góc tương ứng)
Lại có: $\widehat{AMC}+\widehat{CMP}+\widehat{DMP}=180^o$ (kề bù)
$\to\widehat{AMC}+\widehat{CMP}+\widehat{AMI}=180^o=\widehat{IMP}$
$\to$ I, M , P thẳng hàng