Toán Lớp 8: Cho bảng gồm các ô vuông kích thường 5 x 100 (bảng gồm 5 hàng, 100 cột). Người ta tô màu
x
ô vuông đơn vị của bảng sao cho mỗi ô vuông đơn vị của bảng có nhiều nhất 2 ô vuông kề với nó được tô màu (hai ô vuông được gọi là kề nhau nếu chung có một cạnh chung).
Tìm giá trị lớn nhất của
x
.
Leave a reply
Comments ( 1 )
Đáp án bài toán như sau:
Gọi a là số các ô được tô màu nằm ở góc bảng, b là số các ô được tô màu nằm trên cạnh của bảng nhưng không ở góc và c là số các ô vuông còn lại.
Khi đó x = a + b + c
Gọi N là số cặp ô (c1;c2) trong đó c1 là ô được tô màu và c2 là ô kề với ô c1.
Chú ý rằng mỗi ô được tô màu ở góc có 2 ô kề, mỗi ô tô màu ở cạnh có 3 ô kề và mỗi ô đen ở vị trí còn lại có 4 ô kề. Ta có:
N = 2a + 3b + 4c.
Rõ ràng a
≤
4 và b
≤
202.
Do đó N = 4(a + b + c) – (2a + b)
≥
4(a + b + c) – (2.4 + 202) = 4x – 210.
Mặt khác, do mỗi ô vuông của bảng có tối đa 2 ô được tô màu kề với nó nên ứng với mỗi ô vuông sẽ cho tương ứng tối đa 2 cặp (c1;c2) với tính chất như trên.
Do bảng có 500 ô vuông nên N
≤
500.2 = 1000.
Tóm lại, ta có: 1000
≥
4x – 210, hay x
≤
605
2
.
Vì n là số tự nhiên nên x
≤
302.
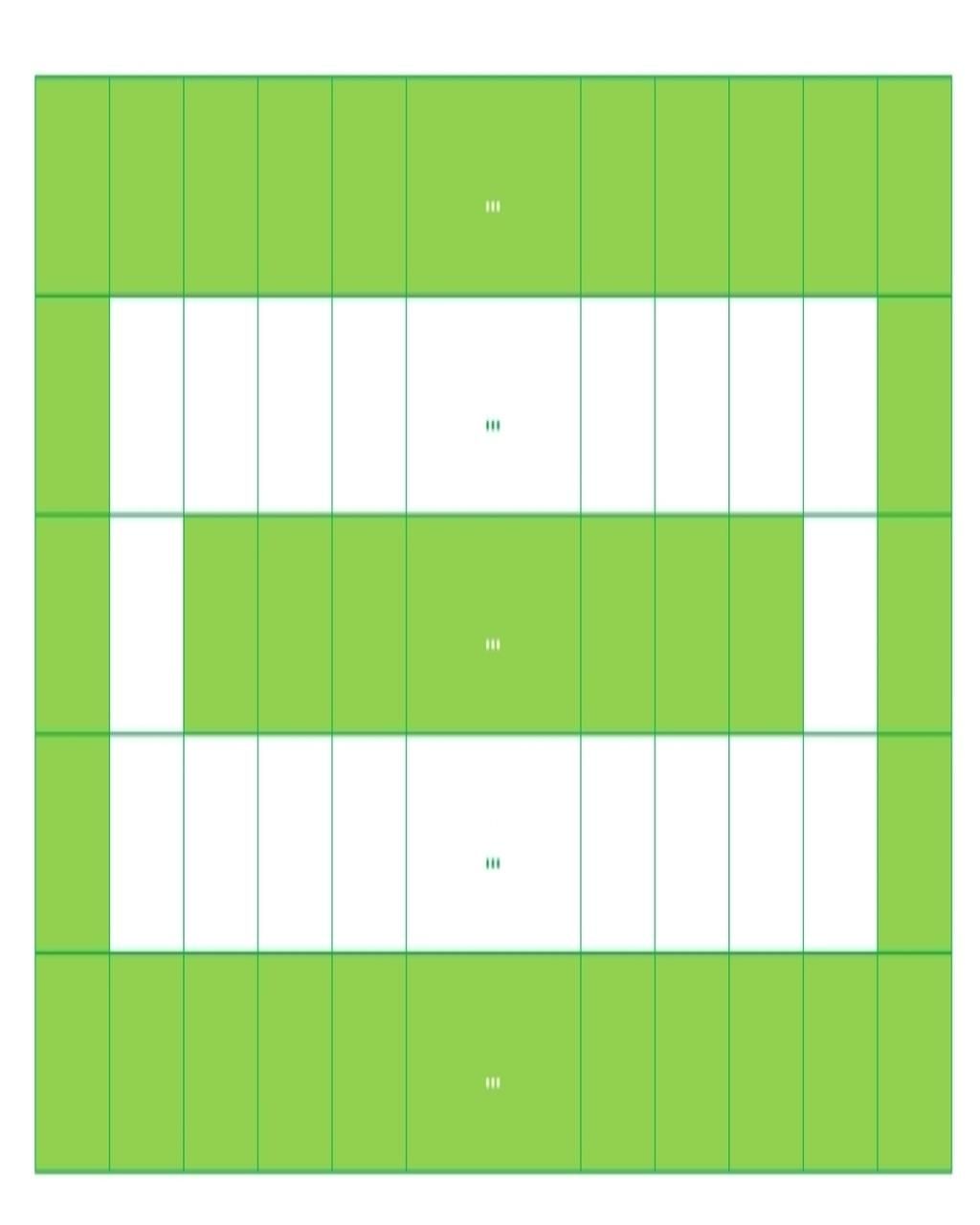
Ta có cách tô dưới đây chứng tỏ có thể tô được 302 ô theo yêu cầu:
Vậy x lớn nhất là 302.
